How To Draw Normal Distribution With Z Statistic Two Tail

Probability and Statistics > Normal Distributions > Ii Tailed Normal Bend

2 Tailed Normal Curve: How to find the area

A two tailed normal curve is one where there's an area in each of the two tails. In order to detect the area for a 2 tailed normal bend, yous have to read a z-table.

Watch the video for an example:

Two Tailed Normal Curve Observe the Area

Can't see the video? Click here.

Z-tables are lists of percentages. The total area nether a normal curve is 100%(1.) and the z-table lists areas equally a fraction of that per centum. For example, you could expect up a z-score for 60% of a normal curve (.6) or 6% (0.06).

If you lot are looking for other variations on finding areas nether curves, meet the area under a normal distribution curve index. The index lists several variations, like finding areas for right-tailed normal curves or left-tailed normal curves.

Need assistance with a homework question? Check out our tutoring page!

Two Tailed Normal Curve: How to find the area: Steps

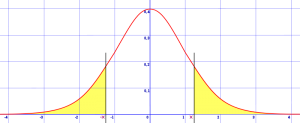
area under a normal distribution curve--two tails

Step i: Expect in the z-table for one of  the given z-values by finding the intersection. For example, if you lot are asked to discover the area in the tail to the left of z = -0.46, look up 0.46.* The table beneath illustrates the result for 0.46 (0.four in the left paw column and 0.06 in the summit row. the intersection is .1772).

z	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.0000	0.0040	0.0080	0.0120	0.0160	0.0199	0.0239	0.0279	0.0319	0.0359
0.1	0.0398	0.0438	0.0478	0.0517	0.0557	0.0596	0.0636	0.0675	0.0714	0.0753
0.2	0.0793	0.0832	0.0871	0.0910	0.0948	0.0987	0.1026	0.1064	0.1103	0.1141
0.iii	0.1179	0.1217	0.1255	0.1293	0.1331	0.1368	0.1406	0.1443	0.1480	0.1517
0.four	0.1554	0.1591	0.1628	0.1664	0.1700	0.1736	0.1772	0.1808	0.1844	0.1879
0.five	0.1915	0.1950	0.1985	0.2019	0.2054	0.2088	0.2123	0.2157	0.2190	0.2224

Pace ii: Decrease the z-value you just constitute in pace 1 from 0.500. In this example, if y'all found .1772 every bit your z-value, and then 0.500 – .1772 = .3228. Fix this number aside for a moment.

Pace 3: Repeat steps ane and 2 for the other tail. For instance, you might accept symmetrical tails (that'due south the most common spread for 2-tailed problems). So if you lot repeat the steps you would get .3228 again.

Stride 4: Add together both z-values together.In this case, the two z-values are .3228 and .3228, so:
.3228 + .3228 = .6456

That'south information technology!

Check out our YouTube channel for hundreds of statistics how to videos and manufactures!

Like the explanation? The Practically Cheating Statistics Handbook has hundreds more footstep by pace examples!

References

Everitt, B. S.; Skrondal, A. (2010), The Cambridge Lexicon of Statistics, Cambridge Academy Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.

---------------------------------------------------------------------------

Demand help with a homework or test question? With Chegg Study, you can get step-past-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is complimentary!

Comments? Need to postal service a correction? Please mail a comment on our Facebook page .

Source: https://www.statisticshowto.com/two-tailed-normal-curve/

Posted by: youngallind.blogspot.com

Share this post